Как в excel выбрать значение из таблицы соответствующее условию

Как пользоваться функциями подбора параметра и поиска решения в Excel

Функция поиска решения пригодится при необходимости определить неизвестную величину

Табличный процессор Microsoft Excel может выполнять не только простые операции с числами (сложение, умножение), расчет суммы или среднего значения. У этой программы имеется очень мощный функционал, который позволяет решать задачи разной сложности. Например, Эксель может оптимизировать значения в таблице, подставляя их таким образом, чтобы они удовлетворяли определенным критериям. Для этого программа оснащена специальными средствами для анализа данных: первый — это подбор параметра, а второй — поиск решения.

Подбор параметра в Эксель

Это простой инструмент, который во многих случаях действительно выручает. Он варьирует значением в одной ячейке для получения определенного результата в другой. Как это работает?

Разберем на простом примере. Мы с Вами планируем открыть депозит с ежемесячным пополнением. Сейчас у нас на руках есть 10 тыс. у.е., но после окончания срока депозита, через 12 месяцев, хотим иметь капитал в 20 тысяч. Требуется посчитать, какую сумму нужно ежемесячно класть на депозит, чтобы через 12 месяцев накопить сумму в 20 тысяч у.е.

Вот наша таблица с расчетами:

В желтой таблице исходные данные: первый взнос, ежемесячный взнос, процентная ставка и срок вклада. В синем поле – конечный капитал, который мы посчитали с помощью функции БС.

Фактически нам нужно подобрать такое значение в ячейке В3, чтобы в В7 стало 20 000. Используем инструмент «Подбор параметра»:

1. Жмем на ленте Данные – Работа с данными – Анализ «что если» — подбор параметра ;
2. В открывшемся окне задаем данные для настройки:
   • Установить в ячейке: в этом параметре указываем ссылку на наше целевое значение, т.е. «Конечный капитал»;
   • Значение: здесь нужно указать то значение, которое должно быть в целевой ячейке, т.е. нужный результат вычислений. В нашем случае это 20 000;
   • Изменяя значение ячейки: Укажем ссылку на ячейку, значение которой нужно изменять, чтобы подбирать результат. В нашем примере это «Ежемесячный взнос»;

1. Жмем Ок, программа будет искать решение. Когда оно будет найдено, Excel сообщит о завершении подбора. Нажимаем Ок в окне, чтобы принять найденное значение и записать его в ячейку, или Отмена, чтобы оставить все как было.

В нашем примере все сработало отлично, и мы узнали, что для получения капитала в 20 тыс, нужно ежемесячно добавлять на депозит по 736,55 у.е.

Иногда случается, что поиск решения не дал результата, тогда нужно проверить всё ли правильно:

1. Первым делом удостоверьтесь, что целевая ячейка зависит от того значения, которое мы изменяем. Если итоговая формула не ссылается на изменяемое значение – восстановите эту зависимость и повторите поиск;
2. Пробуем поставить в изменяемой ячейке значение ближе к искомому, очень часто это помогает;
3. В Экселе ограничено количество итераций для подобного поиска. Возможно, этого количества не хватило, чтобы найти решение. Пробуем увеличить количество итераций. Для этого жмем Файл – Параметры – Формулы , а там в группе команд «Параметры вычислений» увеличьте предельное число итераций.

1. Осмыслите вычисления, которые предлагаете произвести программе. Точно ли заданные Вами параметры имеют решение? Если не имеют – сделайте их корректными.

Обычно этих шагов хватает, чтобы найти значение, удовлетворяющее наш запрос.

MS Excel, подбор параметра, пример решения алгебраического уравнения третьей степени

Билет 16.

«Подбор параметра» — ограниченный по функционалу вариант надстройки «Поиск решения». Это часть блока задач инструмента «Анализ «Что-Если»».

В упрощенном виде его назначение можно сформулировать так: найти значения, которые нужно ввести в одиночную формулу, чтобы получить желаемый (известный) результат.

Где находится «Подбор параметра» в Excel

Известен результат некой формулы. Имеются также входные данные. Кроме одного. Неизвестное входное значение мы и будем искать. Рассмотрим функцию «Подбора параметров» в Excel на примере.

Необходимо подобрать процентную ставку по займу, если известна сумма и срок. Заполняем таблицу входными данными.

Процентная ставка неизвестна, поэтому ячейка пустая. Для расчета ежемесячных платежей используем функцию ПЛТ.

Когда условия задачи записаны, переходим на вкладку «Данные». «Работа с данными» — «Анализ «Что-Если»» — «Подбор параметра».

В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой (B4). Поле «Значение» предназначено для введения желаемого результата формулы. В нашем примере это сумма ежемесячных платежей. Допустим, -5 000 (чтобы формула работала правильно, ставим знак «минус», ведь эти деньги будут отдаваться). В поле «Изменяя значение ячейки» — абсолютная ссылка на ячейку с искомым параметром ($B$3).

После нажатия ОК на экране появится окно результата.

Чтобы сохранить, нажимаем ОК или ВВОД.

Функция «Подбор параметра» изменяет значение в ячейке В3 до тех пор, пока не получит заданный пользователем результат формулы, записанной в ячейке В4. Команда выдает только одно решение задачи.

Решение уравнений методом «Подбора параметров» в Excel

Функция «Подбор параметра» идеально подходит для решения уравнений с одним неизвестным. Возьмем для примера выражение: 20 * х – 20 / х = 25. Аргумент х – искомый параметр. Пусть функция поможет решить уравнение подбором параметра и отобразит найденное значение в ячейке Е2.

В ячейку Е3 введем формулу: = 20 * Е2 – 20 / Е2.

А в ячейку Е2 поставим любое число, которое находится в области определения функции. Пусть это будет 2.

Запускам инструмент и заполняем поля:

«Установить в ячейке» — Е3 (ячейка с формулой);

«Значение» — 25 (результат уравнения);

«Изменяя значение ячейки» — $Е$2 (ячейка, назначенная для аргумента х).

Найденный аргумент отобразится в зарезервированной для него ячейке.

Решение уравнения: х = 1,80.

Функция «Подбор параметра» возвращает в качестве результата поиска первое найденное значение. Вне зависимости от того, сколько уравнение имеет решений.

Если, например, в ячейку Е2 мы поставим начальное число -2, то решение будет иным.

Функции программы Microsoft Excel: подбор параметра

Очень полезной функцией в программе Microsoft Excel является Подбор параметра. Но, далеко не каждый пользователь знает о возможностях данного инструмента. С его помощью, можно подобрать исходное значение, отталкиваясь от конечного результата, которого нужно достичь. Давайте выясним, как можно использовать функцию подбора параметра в Microsoft Excel.

Скачать последнюю версию Excel

• Суть функции
• Применение функции на практике
• Решение уравнений

Суть функции

Если упрощенно говорить о сути функции Подбор параметра, то она заключается в том, что пользователь, может вычислить необходимые исходные данные для достижения конкретного результата. Эта функция похожа на инструмент Поиск решения, но является более упрощенным вариантом.

Её можно использовать только в одиночных формулах, то есть для вычисления в каждой отдельной ячейке нужно запускать всякий раз данный инструмент заново.

Кроме того, функция подбора параметра может оперировать только одним вводным, и одним искомым значением, что говорит о ней, как об инструменте с ограниченным функционалом.

Применение функции на практике

Для того, чтобы понять, как работает данная функция, лучше всего объяснить её суть на практическом примере. Мы будем объяснять работу инструмента на примере программы Microsoft Excel 2010, но алгоритм действий практически идентичен и в более поздних версиях этой программы, и в версии 2007 года.

Имеем таблицу выплат заработной платы и премии работникам предприятия. Известны только премии работников. Например, премия одного из них — Николаева А. Д, составляет 6035,68 рублей. Также, известно, что премия рассчитывается путем умножения заработной платы на коэффициент 0,28. Нам предстоит найти заработную плату работников.

Для того, чтобы запустить функцию, находясь во вкладке «Данные», жмем на кнопку «Анализ «что если»», которая расположена в блоке инструментов «Работа с данными» на ленте. Появляется меню, в котором нужно выбрать пункт «Подбор параметра…».

После этого, открывается окно подбора параметра. В поле «Установить в ячейке» нужно указать ее адрес, содержащей известные нам конечные данные, под которые мы будем подгонять расчет.

В данном случае, это ячейка, где установлена премия работника Николаева. Адрес можно указать вручную, вбив его координаты в соответствующее поле.

Если вы затрудняетесь, это сделать, или считаете неудобным, то просто кликните по нужной ячейке, и адрес будет вписан в поле.

В поле «Значение» требуется указать конкретное значение премии. В нашем случае, это будет 6035,68. В поле «Изменяя значения ячейки» вписываем ее адрес, содержащей исходные данные, которые нам нужно рассчитать, то есть сумму зарплаты работника. Это можно сделать теми же способами, о которых мы говорили выше: вбить координаты вручную, или кликнуть по соответствующей ячейке.

Когда все данные окна параметров заполнены, жмем на кнопку «OK».

Подобную операцию можно проделать и для других строк таблицы, если известна величина премии остальных сотрудников предприятия.

Решение уравнений

Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.

Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.

В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».

Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».

В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2).

В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46.

В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».

Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.

Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Максимальное значение с условиями.

Довольно часто случается, что из большого объёма данных нужно выбрать максимальное значение из какой-то его части. К примеру, найти самую большую партию какого-то определённого товара в огромном списке продаж. Или же найти наивысшую оценку по какому-то предмету среди большого набора данных оценок, набранных учащимися определенного класса по нескольким предметам в школе.

Если вы хотите получить максимальное значение с учётом каких-то условий, вы можете выбрать из нескольких предложенных ниже формул. Чтобы убедиться, что все они возвращают одинаковый результат, мы протестируем их на одном и том же наборе данных.

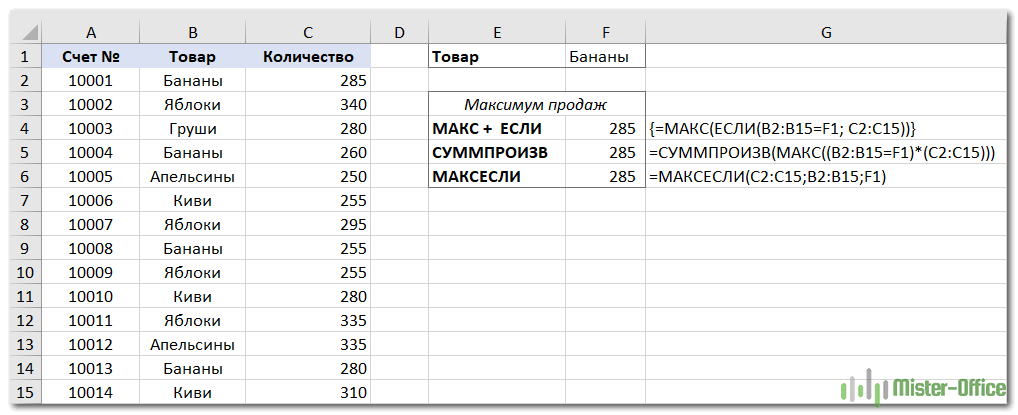
Задача: мы хотим найти самую большую продажу для определенного товара, указанного в F1.

МАКС + ЕСЛИ

Если вы ищете решение, которое работает во всех версиях Excel, используйте функцию ЕСЛИ для проверки условия, а затем передайте полученный массив в функцию:

Чтобы это работало, необходимо нажать Ctrl + Shift + Enter одновременно, чтобы ввести как формулу массива. Если все сделано правильно, Excel заключит ваше выражение в {фигурные скобки}, что является визуальным указанием на формулу массива.

Также можно оценить несколько условий одновременно, о чем мы поговорим далее.

МАКС + СУММПРОИЗВ

Если вам не нравится использовать формулы массива в ваших листах, объедините МАКС с функцией СУММПРОИЗВ, которая умеет работать с массивами:

МАКСЕСЛИ

В Excel 2019 и Office 365 есть специальная функция МАКСЕСЛИ, которая предназначена для поиска наибольшего значения по 126 критериям.

В нашем случае используется только одно условие, поэтому формула очень проста:

На приведенном ниже скриншоте показаны все 3 формулы в действии:

Получить максимальное значение без учета нулей

Фактически, это разновидность условного МАКС, рассмотренного в предыдущем примере. Чтобы исключить нули, используйте логический оператор «не равно» и поместите выражение «<> 0» либо в критерий функции МАКСЕСЛИ, либо в конструкцию МАКС + ЕСЛИ.

Как вы понимаете, проверка этого условия имеет смысл только в случае наличия отрицательных чисел. Для положительных чисел эта проверка излишняя, потому что любое положительное число больше нуля.

Чтобы попробовать, давайте найдем самую маленькую скидку в диапазоне C2:C7. Поскольку все скидки представлены отрицательными числами, наименьшая скидка фактически является наибольшим значением.

Обязательно нажмите , чтобы правильно заполнить эту формулу массива:

А это обычная формула –

И вот что у нас получилось:

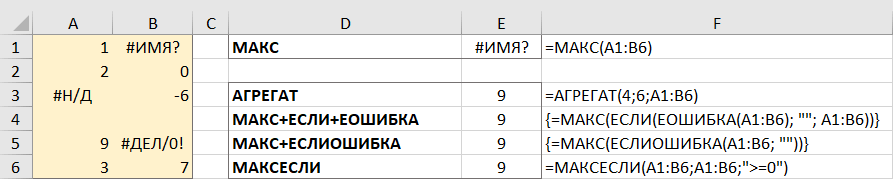
Найдите максимальное значение, игнорируя ошибки

Когда вы работаете с большим объемом данных, управляемых различными формулами, есть вероятность, что некоторые из них приведут к ошибкам. Соответственно, функция МАКС тоже вернет ошибку.

В качестве обходного пути можно использовать МАКС вместе с ЕОШИБКА. Учитывая, что вы ищете в диапазоне A1: B5, формула принимает следующую форму:

Чтобы упростить формулу, используйте функцию ЕСЛИОШИБКА вместо комбинации ЕСЛИ + ЕОШИБКА. Это также сделает логику более очевидной — если есть ошибка в A1:B6, замените ее пустой строкой (»), а затем вычислите самое большое значение в диапазоне:

Неудобство состоит в том, что нужно не забывать нажимать , потому что это работает только как формула массива.

В Excel 2019 и Office 365 функция МАКСЕСЛИ может быть хорошим решением при условии, что ваш набор данных содержит хотя бы одно положительное число или нулевое значение:

Поскольку формула выполняет поиск максимального значения с условием «больше или равно 0», она не будет работать для набора данных, состоящего исключительно из отрицательных чисел.

Также идеально подходит функция АГРЕГАТ, которая может выполнять ряд операций и игнорировать значения ошибок:

Число 4 в первом аргументе предписывает выполнить поиск максимального числа, шестёрка во втором аргументе – это параметр «игнорировать ошибки», а A1: B6 — ваш целевой диапазон.

Все формулы возвращают одинаковый результат:

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

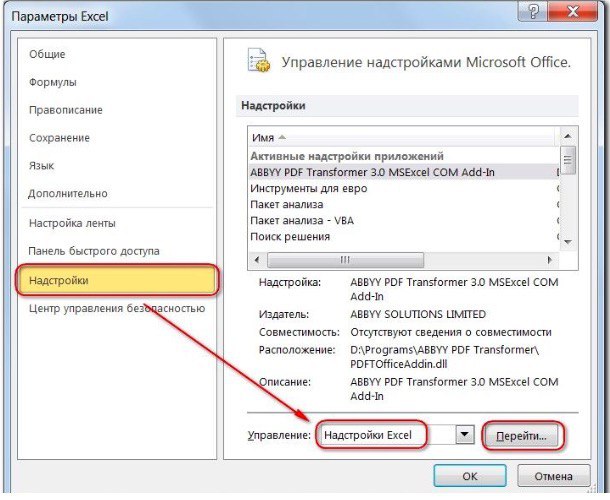
• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

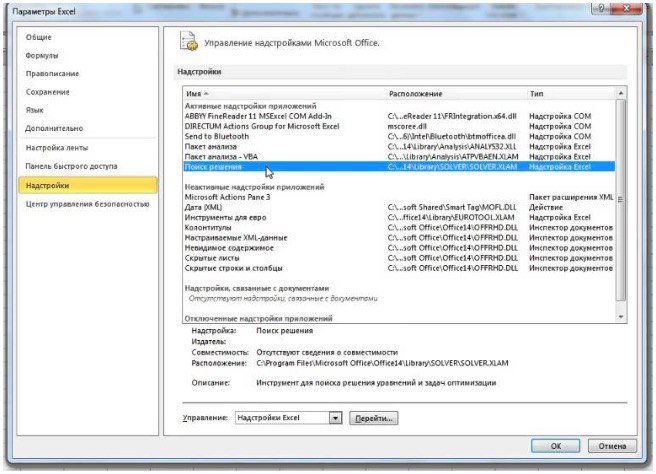
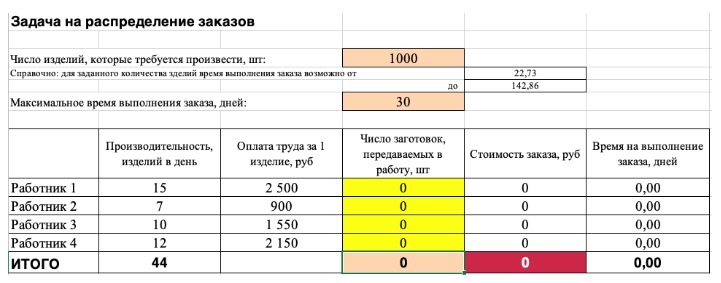
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.

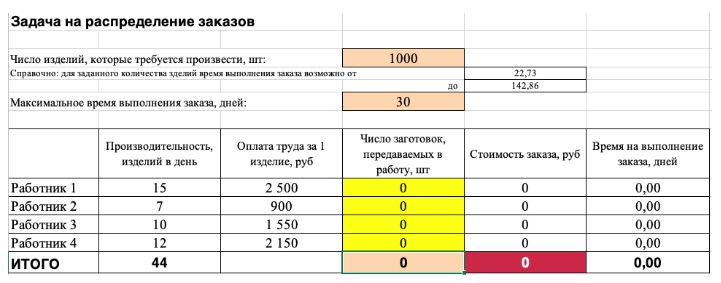
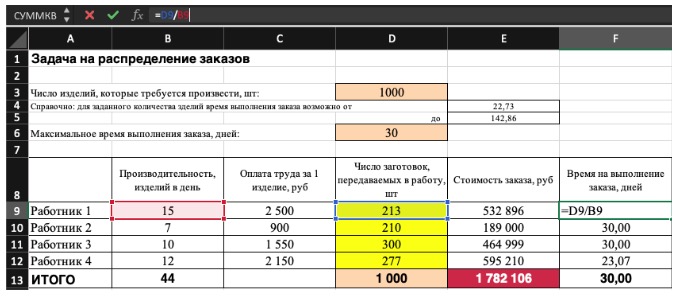
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

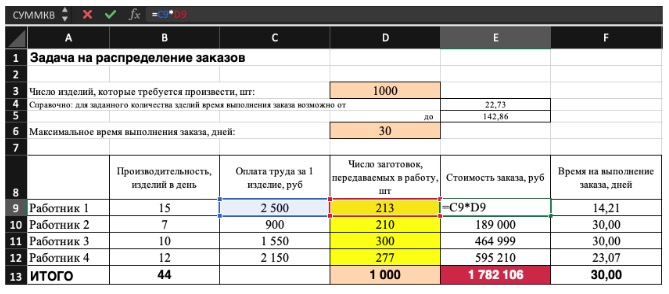
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

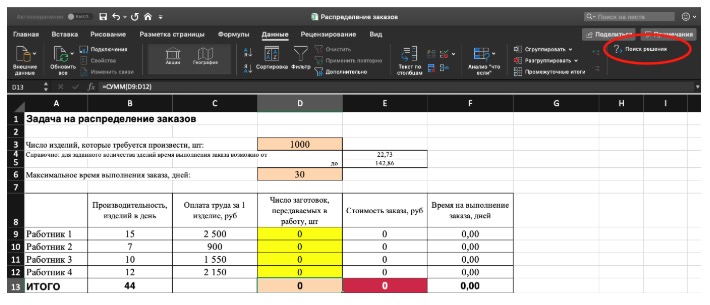
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Функция ВЫБОР в Excel: примеры

Функция ВЫБОР решает задачи по представлению значений из списка в Excel. Например, диапазон А2:А8 содержит номера недели от 1 до 7. Необходимо отобразить день недели прописью, то есть «понедельник», «вторник», «среда», «четверг», «пятница», «суббота», «воскресенье».

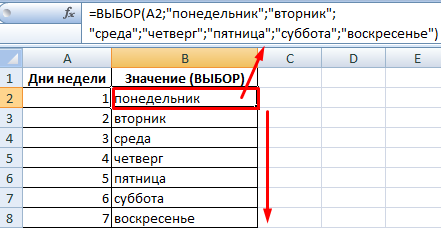
По такому же принципу можно выводить отметки, баллы, времена года прописью.

Теперь рассмотрим можно склонять слова с помощью Excel. Например, слово «рубль»: «0 рублей», «1 рубль», «2 рубля», «3 рубля», «4 рубля», «5 рублей» и т.д.

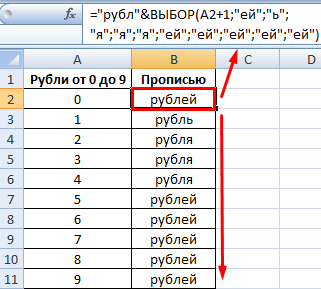
С помощью функции ВЫБОР можно вернуть ссылку на диапазон. Это позволяет делать вычисления над массивами данных по заданному пользователем критерию. Рассмотрим пример суммирования выручки в заданном пользователем магазине.

Имеются данные по выручке в нескольких торговых точках:

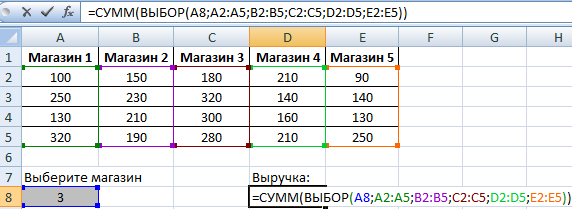
Формула рассчитывает выручку в магазине, заданном пользователем. В ячейке А8 можно изменить номер торговой точки –ВЫБОР вернет для функции СУММ ссылку на другой интервал. Если поставить в ячейке А8 цифру 2, формула подсчитает выручку для второго магазина (результат СУММ для диапазона В2:В5).

С помощью функции ВЫБОР можно задать аргумент для функции СУММ так, чтобы получить результат подсчета 2, 3, 4 и т.д. первых значений диапазона:

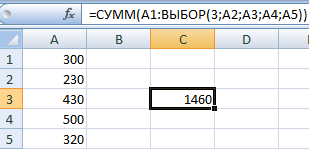
Формула суммирует диапазон А1:А4. Вторая часть диапазона функции СУММ задана с помощью функции ВЫБОР.

Данная функция хорошо обрабатывает в качестве значений простые списки чисел. Поэтому с ее помощью можно вычислить по номеру месяца финансовый квартал.

Таблица с номерами месяцев и кварталов:

Так как финансовый год начался в апреле, месяцы 4, 5 и 6 попали в первый квартал. При введении аргументов функции, номера кварталов необходимо вводить в том порядке, в каком они находятся в таблице.

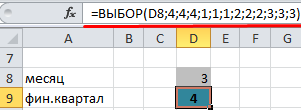
В ячейку D8 пользователь вводит номер месяца. В ячейке D9 функция ВЫБОР вычисляет номер финансового квартала.

Можно так же вычислять грядущие даты. Эту задачу она решает в совокупности с функцией ДЕНЬНЕД. Например, пользователь делает небольшие отчеты о проделанной работе и сдает их начальнику каждый вторник. Можно рассчитать дату следующего вторника.

В первом столбце вспомогательной таблицы – номера дней недели. В третьем столбце – количество дней, которое нужно прибавить к текущей дате, чтобы получить следующий вторник. Например, к понедельнику необходимо добавить 1 день, ко вторнику – 7 дней (до следующего вторника).

В ячейку F2 запишем текущую дату (СЕГОДНЯ()). А в ячейку F3 – формулу для расчета даты следующего вторника:

Индекс определяется с помощью функции ДЕНЬНЕД, которая возвращает для заданной даты соответствующего дня недели.

Использование инструментов от разработчика

Альтернативный вариант создания списка в экселе – это использование ActiveX. В сравнении с первым решением, инструкция немного сложнее, поскольку список опций несколько шире: разрешено задавать большое количество элементов, менять внешний вид списков.

Инструкция по использованию инструментов от разработчика следующая:

1. Активировать опции, поскольку они автоматически отключены. Для этого нужно перейти в меню «Файл».

2. В списке слева найти меню «Параметры» и кликнуть по нему.

3. Открыть раздел с настройками ленты и перейти к «основным вкладкам», поставить галочку напротив разработчика. Остается кликнуть на ОК, чтобы сохранить опции.

4. Должна появиться новая вкладка «Разработчик», через которую можно будет отслеживать рабочий процесс. Для начала создается столбик с элементами, которые выполняют функцию исходных данных для создания выпадающего списка.

5. Перейти в «Разработчик». В подпункте элементов управления кликнуть на кнопку вставки. В появившемся окне выбрать опцию «элементы ActiveX» и кликнуть на значок «Поле со списком».

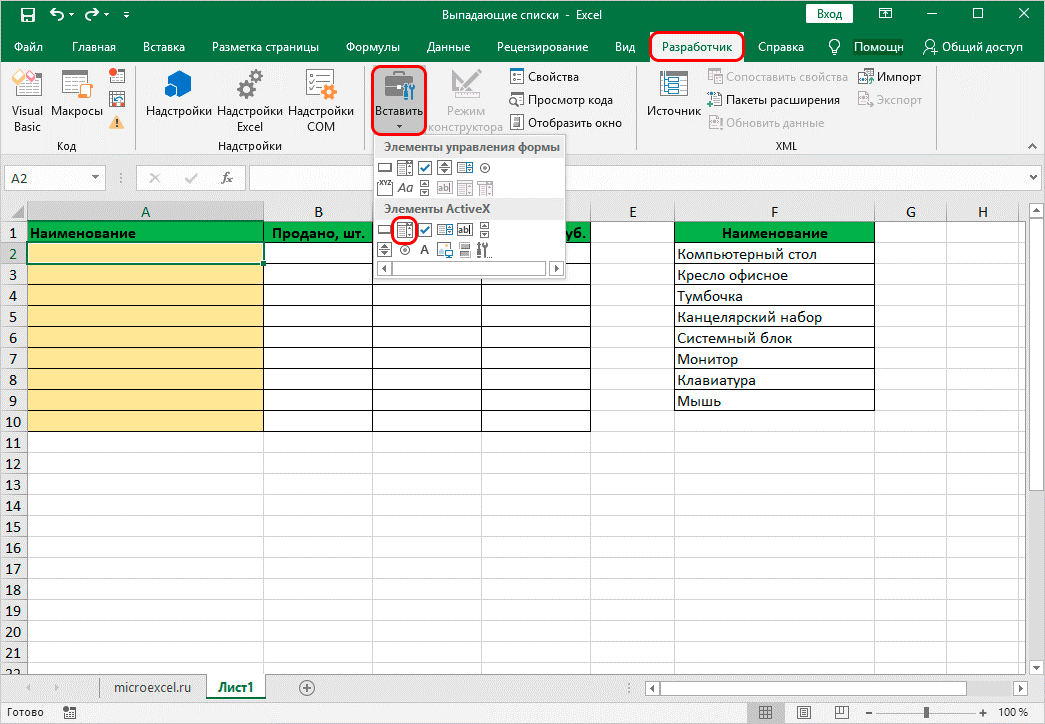
6. Нажать на нужную ячейку, чтобы появилось окно со списком. По желанию можно настроить параметры и границы. При выделении списка, на панели инструментов появится «режим конструктора». Нажать на «Свойства», если требуется продолжить настройку.

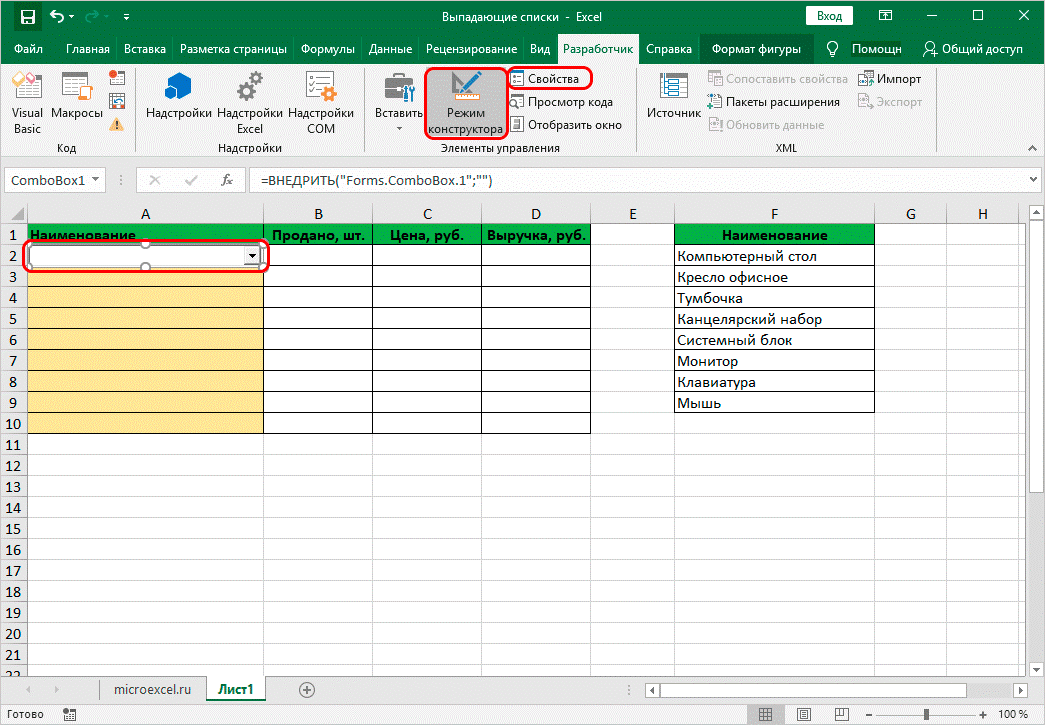
7. В параметрах найти ListFillRange. В столбике поставить рядом «:» и описать координаты ячеек, чтобы создать определенный диапазон. Закрыть окно.

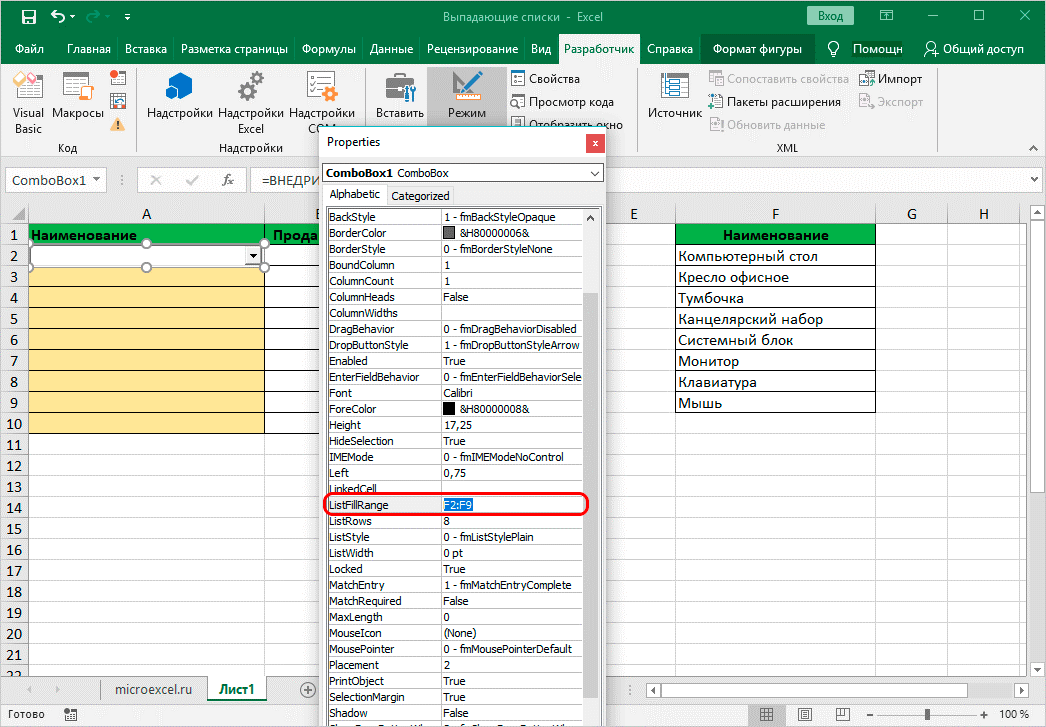
8. Правой кнопкой мышки кликнуть на список в окне, выбрать «объект ComboBox» и кликнуть на edit.

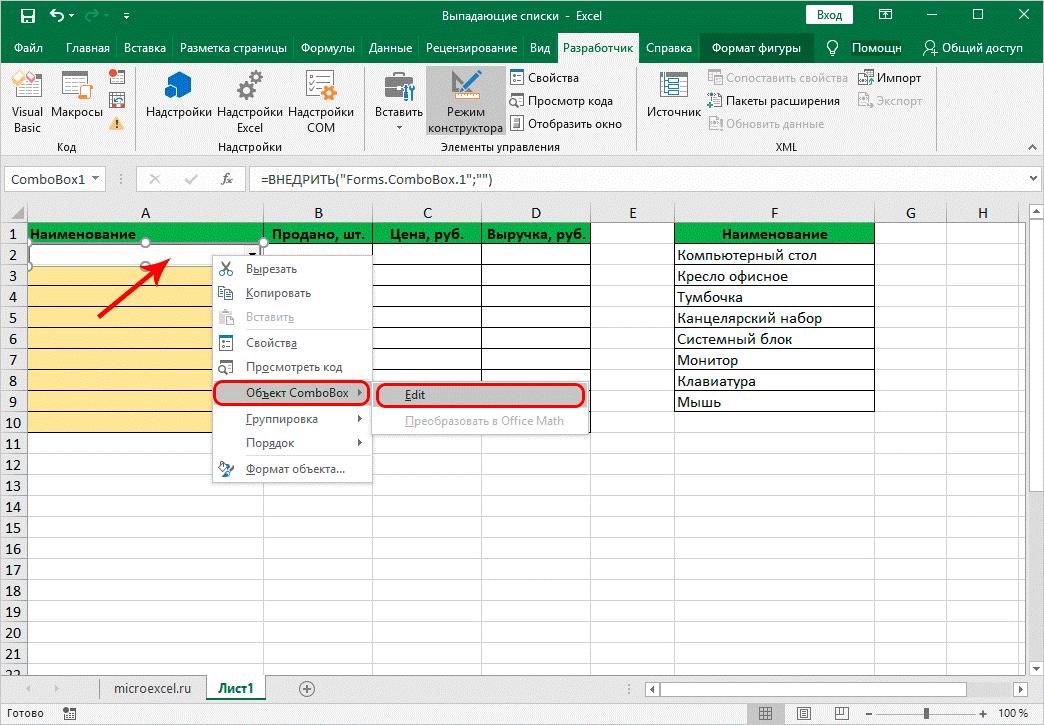
9. Должен появиться список с заранее заданным параметрами.

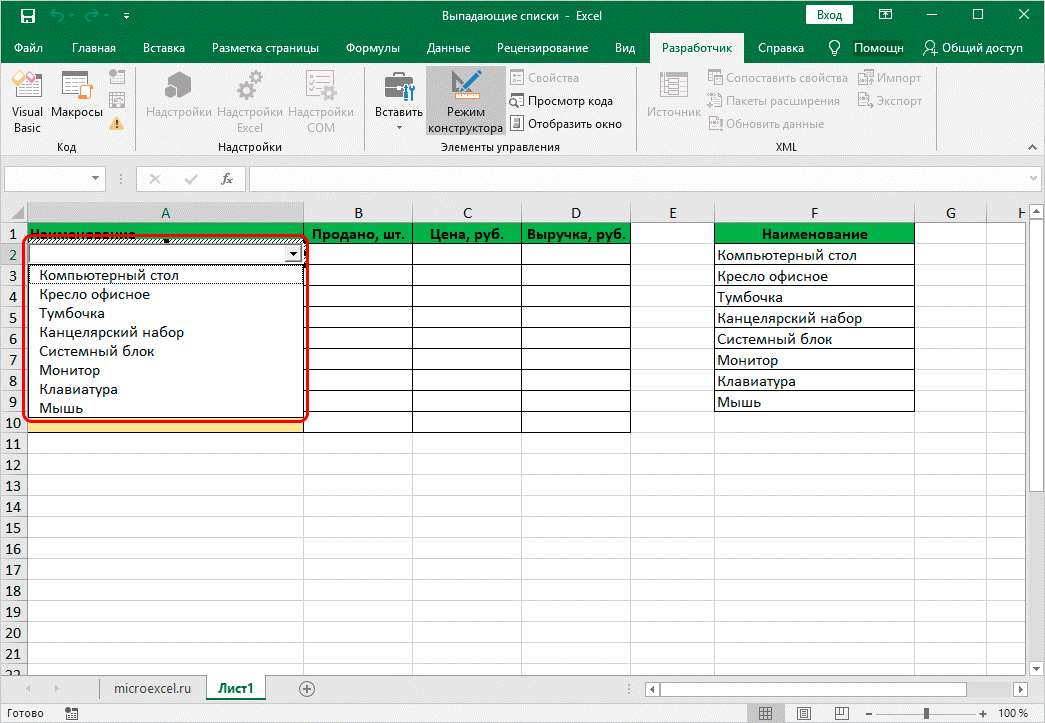
10. Если требуется сделать вставку списка в несколько ячеек, но понадобится навести курсор в правой части нижнем углу страницы. Далее зажать левую кнопку мыши и потянуть вниз до строки, где должен присутствовать список.

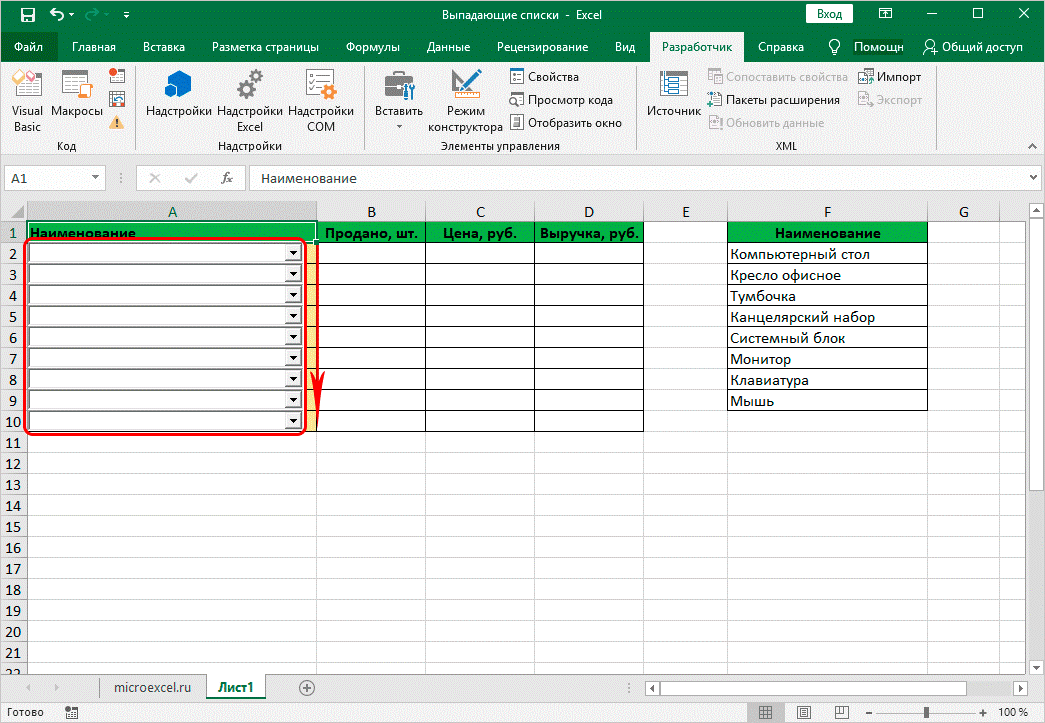
На этом миссию можно считать выполненной. Список будет отображаться в заранее заданных ячейках.
Как сделать связанный список

Данный вариант подойдет пользователям, которые нуждаются в создании сложных и зависимых списков. При выполнении ниже описываемых пунктов, список из одной ячейки будет зависеть от значения другого:

• минимальное количество столбиков – три. В первом указываются наименования, второй и третий – для единиц или количества. При необходимости можно задавать большее количество столбиков;

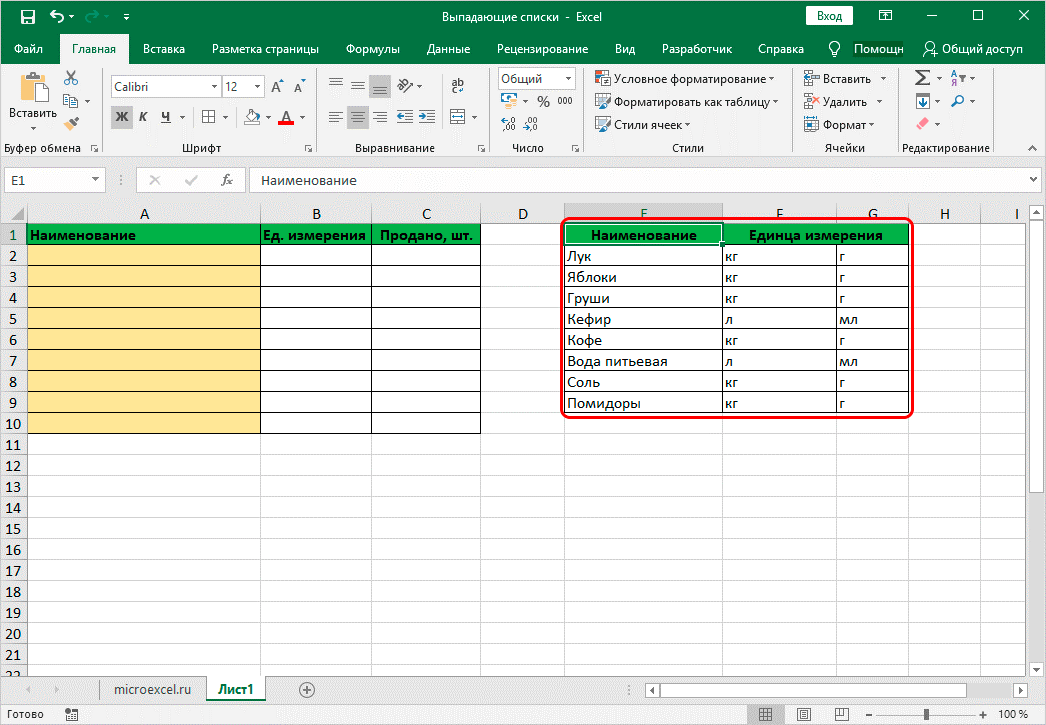
• для начала создается один, общий список для всех названий. Выделяются ячейки с наименованиями посредством контекстного меню;

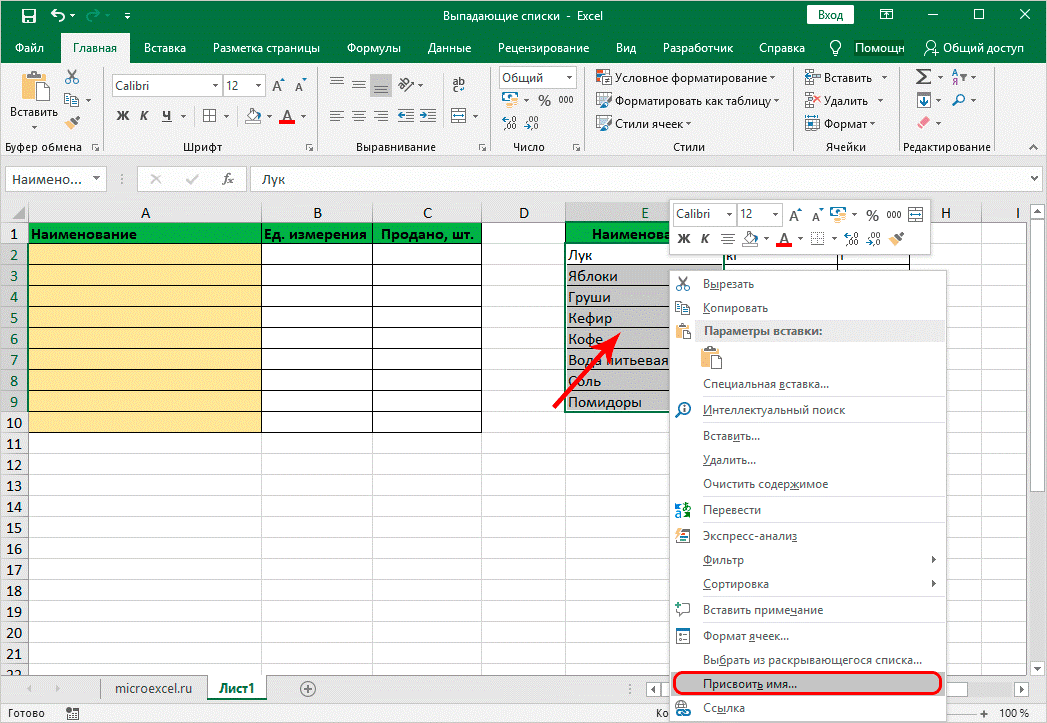
• задать определенное имя;

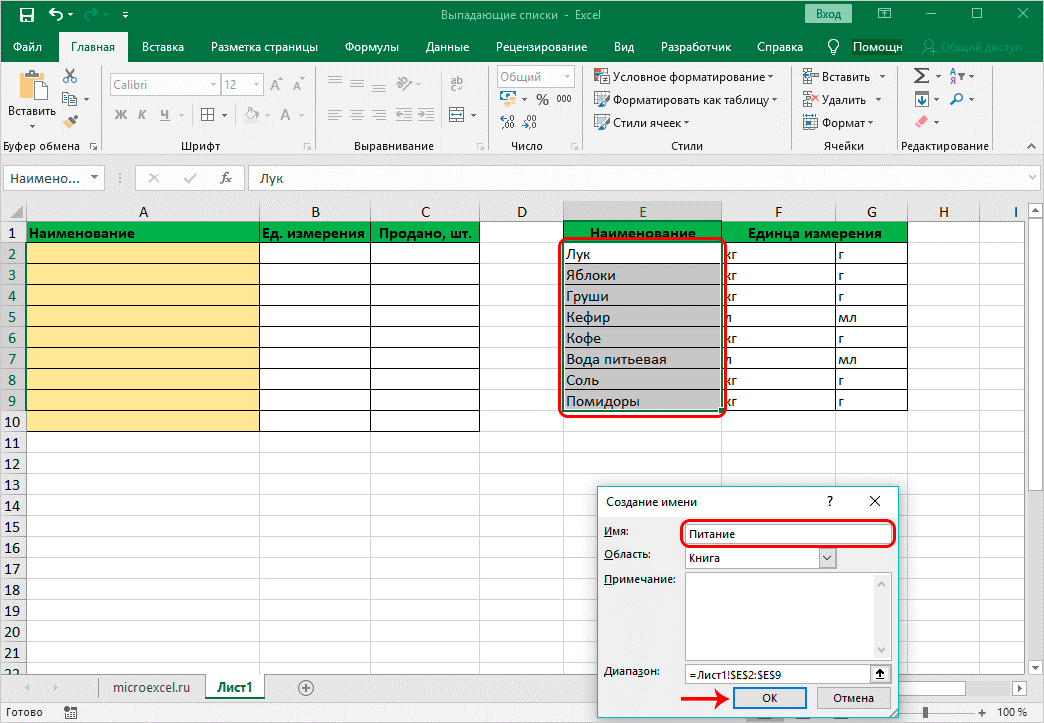
• по аналогии формируются отдельные списки для каждого наименования с определением количества единиц;

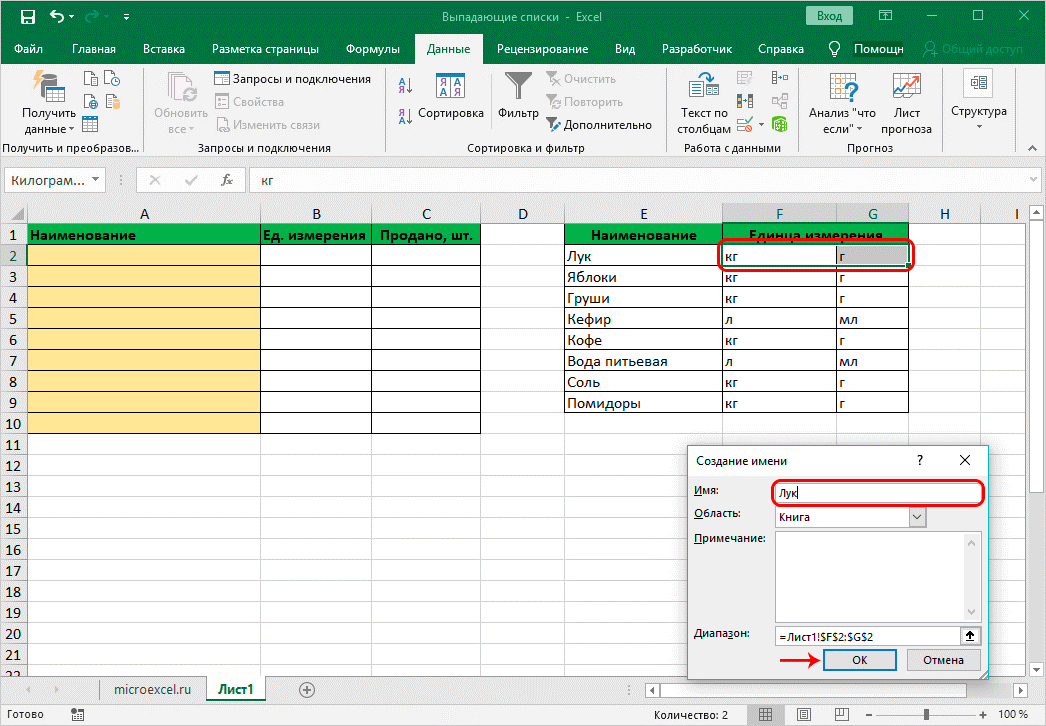
• далее потребуется вставить общий список с наименованиями в верхней ячейке в первом столбике главной страницы;

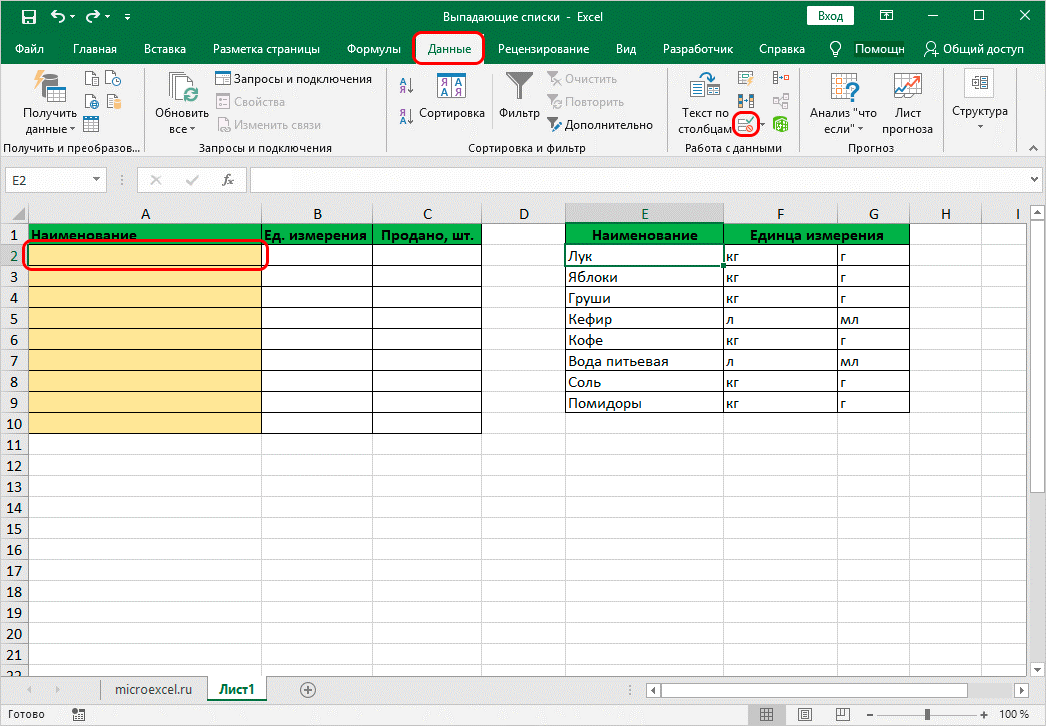
• указать в качестве основного источника ранее заданную таблицу;

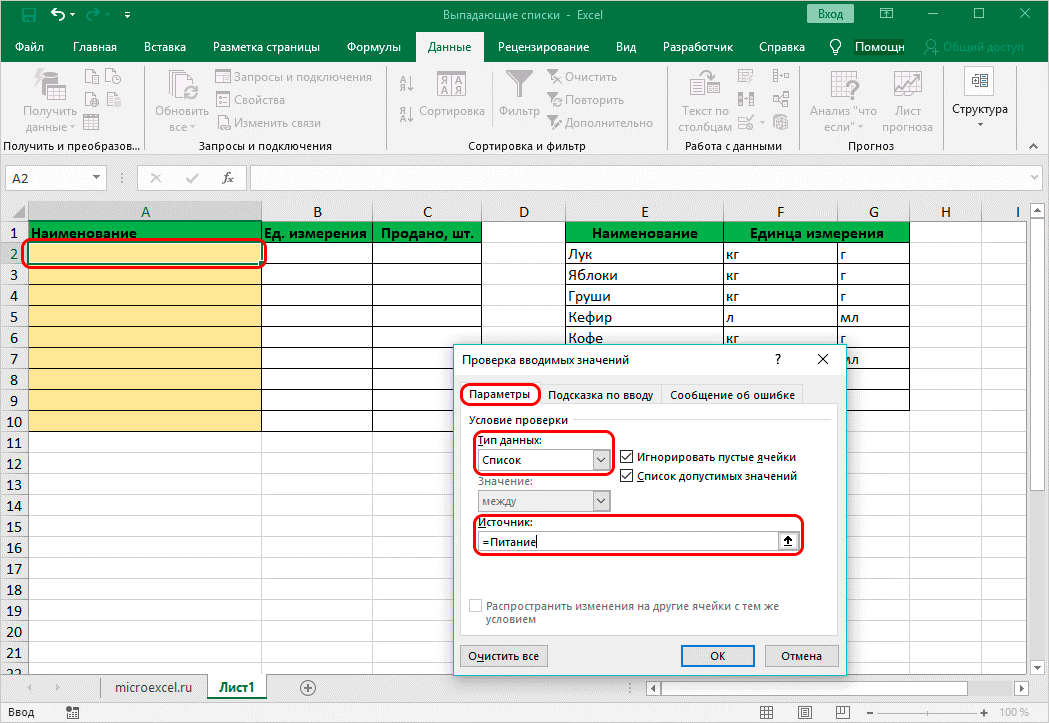
• кликнуть по верхней части столбика, где указаны единицы измерения, зайти в проверочное окно и в источнике указать «=ДВССЫЛ(A2)», вместо А2 может быть любая ячейка с наименованием продукта;

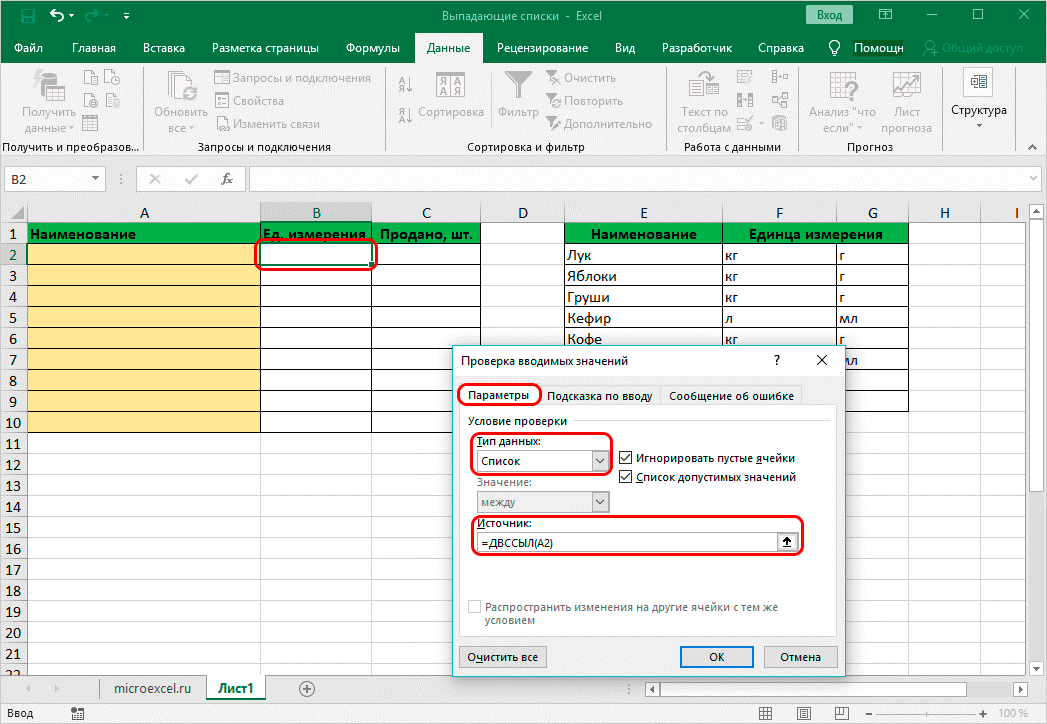
• список готов. Теперь можно растянуть по желанию строки и таблицы.

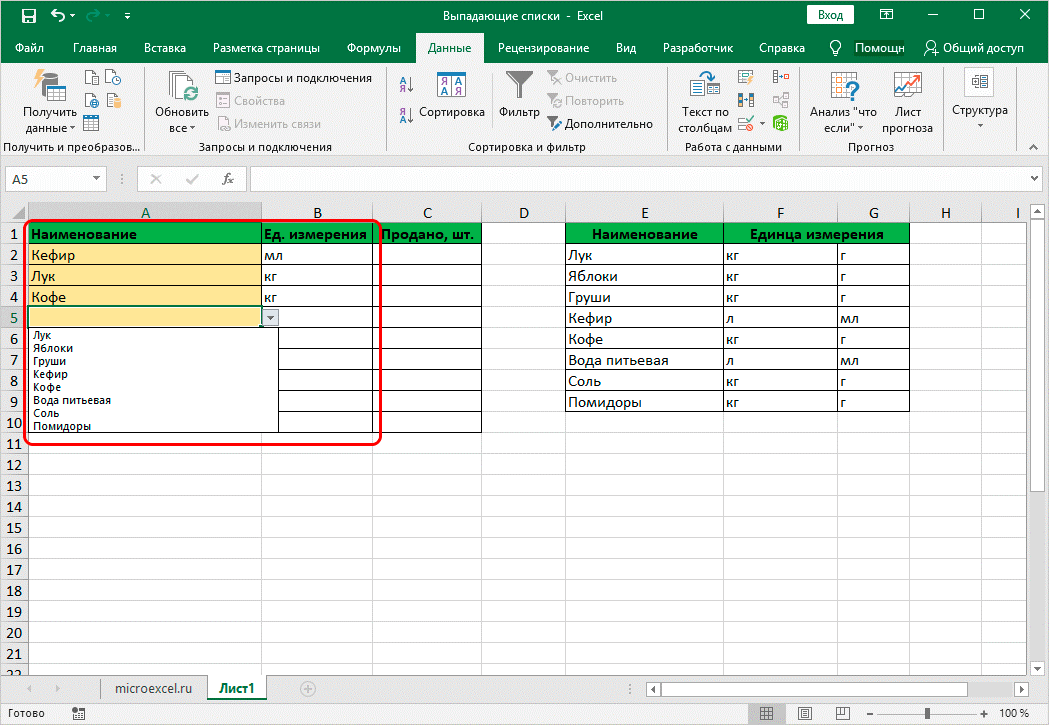
Создавая выпадающие списки, каждый пользователь может облегчить ведение отчетности в экселе. Каждая представленная инструкция имеет свои преимущества и не отнимет много времени, чтобы должным образом структурировать всю информацию.

Вывод отобранных строк в таблицу

Теперь осталось вывести на экран выборку учеников класса с нужной оценкой. Для этого сопоставим номера в столбце F с номерами в технической колонке D. Удобнее всего это сделать с помощью комбинации функций ИНДЕКС и ПОИСКПОЗ:

Алгоритм работы на примере ячейки G3:

1. Функция ПОИСКПОЗ получает числовой индекс строки из ячейки F3 и ищет такое же значение в техническом столбце D. Возвращает либо порядковый номер найденной ячейки в массиве, либо ошибку #Н/Д
2. Функция ИНДЕКС получает из ведомости класс, находящийся в ячейке, порядковый номер которой мы получили в первом пункте
3. Далее функция ЕСЛИОШИБКА выводит на экран класс, если он найден, или пустую строку, если ПОИСКПОЗ вернула ошибку

Такой порядок работает и для остальных столбцов: «Фамилия», «Баллы». Теперь если изменить искомый класс или оценку, формулы сами всё пересчитают и переформируют список. Можно скрыть дополнительный столбец, чтобы не мешал.

Для удобного выбора оценки и класса, я создал раскрывающийся список. В этой статье вы можете прочитать, как это делается.

Мы получили полностью автоматизированный интерактивный проект, способный формировать списки «налету», сразу после того, как вы сделаете свой выбор. На этом всё, и я готов отвечать на ваши вопросы!