Поиск решения в excel скачать надстройку

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Расположение

Немногие знают, где находится данная функция. Во вкладке Данные на главное панели можно обнаружить одноименную кнопку. Стоит отметить, что поиск решения является надстройкой excel и не у всех пользователей она включена. Чтобы активировать инструмент, нужно сделать следующее:

1. Нажимаете кнопку Office в верхнем левом углу экрана и переходите к Параметрам.

2. Ищете строку Надстройки и в правой части диалогового окна нажимаете кнопку Перейти. Обязательно проверьте, чтобы левее была надпись Надстройки Excel.

3. Ставите галочку напротив Поиск решения и нажимаете ОК.

4.Программа выдает предупреждение об отсутствии компонента и предлагает его установить. Соглашаетесь.

5. Дожидаетесь окончания установки.

6. Если все сделано правильно, то во вкладке Данные появится блок Анализ с кнопкой Поиск решения.

Простой пример использования Поиска решения

Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.

Данные модели организуем следующим образом (см. файл примера ).

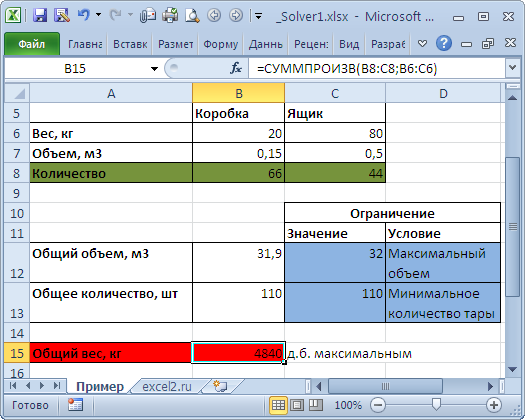
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.

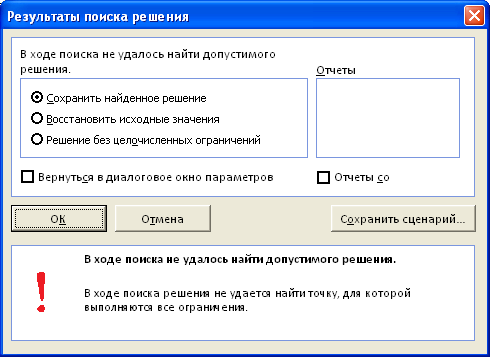
При ограничении 17 м3 Поиск решения найдет решение.

Подготовка оптимизационной модели в MS EXCEL

Поиск решения оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне Поиска решения возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.

Совет. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки Поиска решения (см. ниже).

Приведем алгоритм работы с Поиском решения, который советуют сами разработчики ( www.solver.com ):

• Определите ячейки с переменными модели (decision variables);
• Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
• Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
• С помощью диалогового окна Поиск решения введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
• Запустите Поиск решения для нахождения оптимального решения.

Проделаем все эти шаги на простом примере.

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter – это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Использование

Чтобы нагляднее показать работу инструмента поиск решения, рассмотрим примеры решения задач, с которыми может столкнуться каждый пользователь. Допустим, в наличии имеется некая сумма денежных средств, которую человек готов положить на депозит в банк под фиксированный процент и ежегодно пополнять счет на первоначальную сумму. При этом есть конкретная цель, которую вкладчик хочет достигнуть, по истечении пяти лет.

Перенесем эти сведения на рабочий лист excel.

В отдельном столбце запишем все года по порядку, а в соседнем поле пропишем формулу и воспользуемся маркером автозаполнения. Функция, которая поможет получить первоначальные данные, называется БС и состоит она из следующих основных аргументов:

1. 1. Процентная ставка.
2. 2. Период (кпер).
3. 3. Сумма платежа (плт).

Для первого года формула будет выглядеть следующим образом:

Как видите, число отрицательное – это особенной функции БС. Чтобы этого избежать, ячейку с суммой денег нужно сделать отрицательной. Тогда итоговые результаты будут отображаться корректно.

Воспользуемся автозаполнением и получим сумму средств после 5 лет нахождения на депозите под 4 процента годовых с ежегодным пополнением.

Полученная цифра не удовлетворяет условию в 12000 после пятилетнего периода. Теперь необходимо воспользоваться инструментом Поиск решения. При этом изменяемыми параметрами будет процент и первоначальная сумма. Заполняете диалоговое окно построчно.

Нажимаете кнопку Выполнить и получаете решение задачи с условием достижения поставленной цели за пять лет.

Как видите, изменилась только процентная ставка, хотя изменяемыми величинами были два параметра. Чтобы это исправить, в настройках необходимо поставить галочки напротив строчки Автоматическое масштабирование.

Повторяете решение с новой конфигурацией и получаете следующие данные: Как видите, чтобы достигнуть отметки в 12000$ через пять лет, необходимо найти депозит под 4,03 процента годовых и ежегодно пополнять его на сумму 2214 доллара 01 цент.

В результате использования инструмента Поиск решения, можно быстро подобрать исходные условия, для выполнения поставленной цели, что дает более четкое и математически рассчитанное представление о путях достижения результата.

Решение в MS Excel (надстройка «Поиск решения»).

Рис.э.3. Фрагмент электронных таблиц Excel в режиме отображения данных.

Рис.э.4. Диалоговое окно надстройки «Поиск решения» при поиске оптимального решения.

Рис.э.4. Диалоговое окно надстройки «Поиск решения» при поиске оптимального решения.

Рис э.5. Фрагмент электронных таблиц Excel с отчетом по устойчивости

Экономическая интерпретация множителей Лагранжа

Множитель Лагранжа

В рассмотренном примере

Проверим этот вывод. Пусть в нашей задаче критерий остался прежним, поменялась правая часть ограничения

Решим эту задачу в MS Excel (надстройка «Поиск решения»).

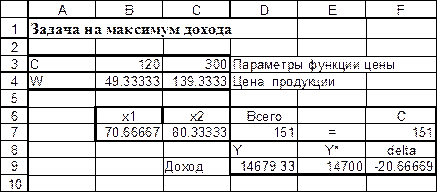
Рис.э.6. Фрагмент электронных таблиц MS Excel в режиме отображения данных.

Стационарная точка

Приращение функции -20,67 оказалось больше по модулю, чем ожидаемое приращение -20. Это объясняется нелинейностью целевой функции и тем, что множитель Лагранжа

Иллюстрация полученного решения в MS Excel.

Чтобы проиллюстрировать полученное решение диаграммами с помощью линий уровня, затабулируем соответствующие функции (рис.э.7). Основную идея -описать решение кв.ур-я. Соответствующая диаграмма приведена на рис.*.10. Эта диаграмма является упрощенным вариантом рис.э.2. Точка соответствующая оптимальным значениям выделена. В ней линия уровня, соответствующая уровню

Рис.э.7. Фрагмент электронных таблиц Excel в режиме отображения данных. Табулирование целевой функций для построения линий уровня.

Рис.э.8. Фрагмент электронных таблиц Excel в режиме отображения формул. Табулирование целевой функций для построения линий уровня.

Чтобы построить семейство линий уровня

С заметим, что линии уровня — вложенные (концентрические) эллипсы.

Рассмотрим процесс построения линии при С =1000. Необходимо построить таблицу значений

Последнее соотношение следует рассматривать как квадратное уравнение относительно

с

Рис.э.9. Линии уровня целевой функции и равного объема.

Функция «Подбор параметра»

Подбор параметра в Excel позволяет подобрать какой-то определенный параметр, значение которого неизвестно. Чтобы было понятней, можно привести такой пример. Допустим, есть прямоугольник со сторонами A и B. Известно, что общая площадь этой фигуры составляет 400 квадратных метров, а сторона B — 40 метров. Сторона A неизвестна и, соответственно, нужно ее найти. Для решения такой задачи необходимо заполнить рабочий лист программы теми данными, которые уже известны. Для этого нужно создать таблицу с 2 колонками и 3 строками (диапазон ячеек A1:B3).

Первый столбец будет содержать название сторон прямоугольника и букву, обозначающую его площадь (т.е. A, B и S). А во втором столбце необходимо указать известные значения:

• в соседней ячейке для стороны B (ячейка B2) написать — 40 (значение для стороны А остается пустым);
• а в соседнем поле для площади прямоугольника (поле B3) написать следующую формулу: = B1*B2 (т.е. формула для расчета площади).

Если все было сделано правильно, то в поле B3 должно быть значение 0. Затем надо выделить эту ячейку и выбрать в панели меню пункты: «Сервис — Подбор параметра». В появившемся окне нужно указать то значение, которое должно быть получено в результате, т.е. 400. В строке «Установить в ячейке» будет указано поле «B3»: менять его не нужно, так и должно быть (сюда будет выведен результат). А в строке «Изменяя значение» необходимо выбрать неизвестный параметр, т.е. поле B1. После нажатия кнопки «ОК» программа выдаст результат: сторона А — 10 метров, а в поле общей площади прямоугольника будет указано число 400.

Это была очень простая задача на уровне 3 класса, но с помощью такой функции можно решать и более сложные задачи. Например, вы решили приобрести себе автомобиль в кредит. Вы точно знаете, что сможете выплачивать ежемесячную выплату в размере 1000 $ (но не больше), а также, что банк выдает автокредит с процентной ставкой 6,5%. Суть задачи заключается в следующем: «Какова максимальная сумма машины, которую можно взять в кредит на таких условиях?». То есть теперь программа будет искать стоимость автомобиля, отталкиваясь от того, что ежемесячный платеж не должен превышать 1000 $. Такой пример является уже более сложным, а также более практичным, нежели расчет площади прямоугольника.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Пересчитать формулы в диапазоне

Выделите диапазон ячеек, в которых необходимо пересчитать формулы. Выберите в меню надстройки ЁXCEL команду «Пересчитать формулы в выделенном диапазоне» и формулу будут пересчитаны только в этом диапазоне, но не в листе и не в книге.

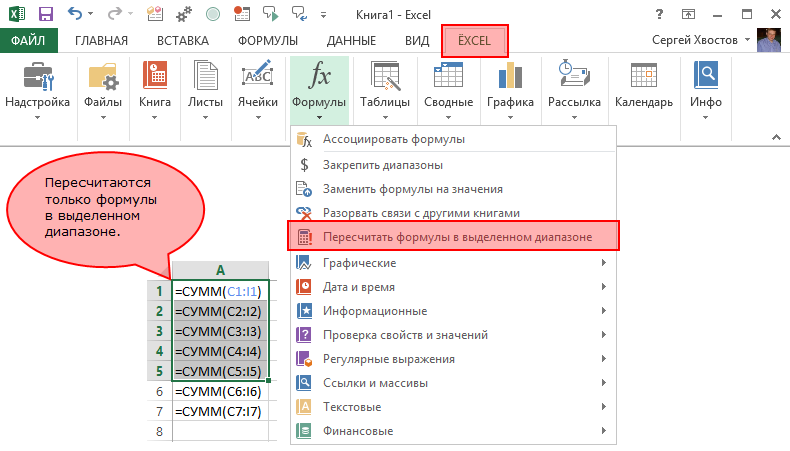
Надстройка ЁXCEL

ОС Windows (RU) MS Excel 2007 — 2019 (RU) Версия: 19.12 119 команд 67 формул Открытый код VBA On-Line консультации Регулярные обновления Для любого количества ПК

Перед скачиванием нажмите Ctrl + F5

Как подключить надстройку ЁXCEL?

Вариант №1, Вариант №2.

Если у Вас возникнут какие-либо вопросы, просто, напишите мне и я постараюсь ответить на них как можно скорее.

Комментарии

Делается средствами самого Excel:1. Жмём F52. Жмём кнопку «Выделить. «3. Ставим галку «пустые ячейки»4. Жмём Ок5. Жмём F26. Водим значение «0» и жмём Ctrl+Enter.P.S. Если заменить нужно только в конкретном диапазоне, то на Шаге 0 его предварительно выделяем.

Делается средствами самого Excel:1. Жмём F52. Жмём кнопку «Выделить. «3. Ставим галку «пустые ячейки»4. Жмём Ок5. Жмём F26. Водим значение «0» и жмём Ctrl+Enter.P.S. Если заменить нужно только в конкретном диапазоне, то на Шаге 0 его предварительно выделяем.

Добрый день Сергей!Спасибо за настройку! хотелось бы поделится с вами своим решением проблемы выше. Инструкция будет детальная и понятная для простого пользователя и помогла мне решить проблему на 3 рабочих станциях. У меня точно так же возникал запрос на сохранение файла при каждом закрытии файлов эксель.

Конкретные примеры использования

Закончив с виртуальным примером, который помог разобраться с особенностями построения таблицы и задачи условий перейдём к более приземлённым и конкретным примерам. С их помощью в задаче будет разобраться немного проще.

Изготовление йогурта

Попробуем рассчитать какой из видов йогурта при разной концентрации компонентов производить лучше, чем остальные. Для этого определим компоненты, их соотношение и стоимость конечного продукта, при условии ограниченности запасов:

В раздел «Расход сырья» внесены формулы, которые опираются на «количество» и нормы расхода. Прибыль является произведением стоимости и количества. Количество и будет переменной, которая будет изменяться в пределах «запасы». Для этого формируется следующий набор условий:

В результате вычислений (с учётом дробного остатка, поскольку условие работы только с целыми числами добавлено не было), получилось, что эффективнее всего производить 1 и 3 йогурты, а второй полностью игнорировать.

Затраты на рекламу

Другим вопросом, с которым поможет эта функция будет «оптимизация расходов на рекламу». В этом случае перед пользователем стоит задача: повысить возможную прибыль посредством изменения рекламных вложений в определённые месяцы.

Итак, прибыль является целевой ячейкой (выделена изумрудным цветом). Зелёным выделены расходы на рекламу, а красным максимальные затраты. При поиске решения ограничиваем подстановку переменных в значениях рекламы максимумом, а в качестве цели ставим максимизацию прибыли.

В результате получаем максимизированную прибыль в указанном месяце, посредством грамотного распределения рекламного бюджета между остальными месяцами.

Отсюда и вытекает главный недостаток «поиска решений». Он оперирует лишь конечной (одной) ячейкой. Чтобы максимизировать прибыль требуется работать с последней ячейкой (прибыль – всего), что сопряжено с вероятностью появления ошибки в программе, если формулы настроены неверно.

Поиск решения в Excel

Поиск решения – это надстройка Excel, позволяющая делать задачи на оптимизацию. Как это работает: у вас есть данные, которые связаны между собой формулами. При этом на какой-то результирующий итог влияют как положительным, так и отрицательным образом. Например, прибыль зависит от расходов на рекламу как положительно (ведь чем больше рекламы, тем больше объем продаж), так и отрицательно (расходы на рекламу увеличивают общие расходы и уменьшают прибыль). В конце статьи будет ссылка на файл, где вы сможете сами посмотреть наглядно таблицу и прорешать параллельно со мной.

Поиск решения путем подбора данных находит наиболее эффективное значение. В нашем случае, максимальную прибыль. Я взял небольшую таблицу: Здесь, как видите, синим обозначена целевая ячейка, та, которую нужно максимизировать, изменяя расходы на рекламу (зеленые ячейки). Хитрость в том, что прибыль зависит от объема продаж (в штуках), а от него, в свою очередь зависят и расходы и доходы, которые формируют прибыль. Т.е., просто увеличив или уменьшив расходы на рекламу, вы не получите лучшего результата. В этом и состоит ценность Поиска решения – он делает перебор всех возможных значений по своему алгоритму и получает наилучший результат. Кто проходил обучение по моему самоучителю , уже в курсе, как это делается и как применяется.

Еще есть ограничение бюджет рекламных расходов в 40 тыс. долл. за 4 месяца.

Итак, приступим к технической части.

1. Если вы никогда не пользовались этой надстройкой, придется ее сначала установить. Дело в том, что по умолчанию Поиск решения не ставится. Заходим Офис/Параметры Excel/Надстройки/Кнопка “Перейти”. Мы уже заходили сюда, когда делали сумму прописью .
2. Теперь, у вас на вкладке Данные появилась команда “Поиск решения”. Нажимаем и видим такое окошко:
3. Целевая ячейка – это там, которую мы хотим максимизировать, это результат. У нас это B15. Т.е. я хочу увидеть, какими должны быть расходы на рекламу, чтобы в январе у меня была максимальная прибыль. Ставим выбор “максимальному значению”.
4. Изменяя ячейки – ставим диапазон ячеек, от которых зависит итог. У меня это все расходы на рекламу, т.е. диапазон B11 – E11.
5. Ограничения – ну без них никак. Excel мыслит больше математически, поэтому нам надо:

• Поставить условия положительности изменяемых ячеек. B11:E11 > 0
• Ограничить рекламный бюджет за 4 месяца. F11=40000

1. Нажимаем на кнопку “Выполнить”. Если что-то пошло не так, а это бывает, обнулите диапазон изменяемых ячеек, может помочь.

В итоге мы получим нужный результат

Если не получим, значит, надо пересмотреть условия, возможно, что-то некорректно проставлено или задача не имеет решения.

Видео по теме (5 минут):

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Обработка «Распознавание штрихкода с помощью утилиты Zbar» для Документооборот ред. 2

В связи с тем, что стандартный функционал программы «Документооборот» ред. 2.1 дает возможность распознавания штрихкодов только форма EAN-13, данная обработка — альтернативный способ для распознавания штрихкода в программе 1С: Документооборот ред. 2 с помощью утилиты Zbar, которая распознает в том числе и в формате Code 128 (один из стандартных штрихкодов кодирования документов, например, «Управление торговлей» ред. 11), а также с возможностью поэтапно проследить все действия от распознавания до прикрепления к документу или простой загрузки в каталоги файлов в базе 1С.

5 стартмани

Установка Поиска решения

Команда Поиск решения находится в группе Анализ на вкладке Данные.

Если команда Поиск решения в группе Анализ недоступна, то необходимо включить одноименную надстройку. Для этого:

• На вкладке Файл выберите команду Параметры, а затем — категорию Надстройки;
• В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти;
• В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.

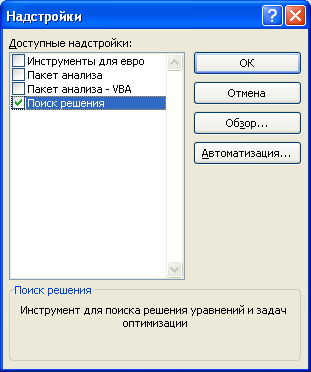
Примечание. Окно Надстройки также доступно на вкладке Разработчик. Как включить эту вкладку читайте здесь.

После нажатия кнопки Поиск решения в группе Анализ, откроется его диалоговое окно.

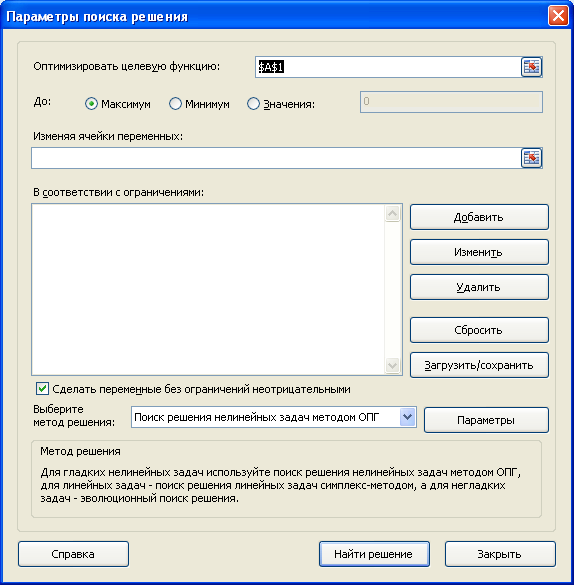
При частом использовании Поиска решения его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт Добавить на панель быстрого доступа.

Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.

Совет. Перед использованием Поиска решения настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.

Ниже приведен небольшой ликбез по этой теме.

Надстройка Поиск решения помогает определить лучший способ сделать что-то:

• «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
• «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.

Вот некоторые типичные примеры оптимизационных задач:

• Определить план производства, при котором доход от реализации произведенной продукции максимальный;
• Определить схему перевозок, при которой общие затраты на перевозку были бы минимальными;
• Найти распределение нескольких станков по разным видам работ, чтобы общие затраты на производство продукции были бы минимальными;
• Определить минимальный срок исполнения всех работ проекта (критический путь).

Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется Поиском решения только по одному показателю (этот оптимизируемый показатель называется целевой функцией). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений. Поиск решения подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.

Примечание. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента Подбор параметра. Перед первым знакомством с Поиском решения имеет смысл сначала детально разобраться с родственным ему инструментом Подбор параметра. Основные отличия Подбора параметра от Поиска решения:

• Подбор параметра работает только с моделями с одной переменной;
• в нем невозможно задать ограничения для переменных;
• определяется не максимум или минимум целевой функции, а ее равенство некому значению;
• эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).

Навигатор по конфигурации базы 1С 8.3

Универсальная внешняя обработка для просмотра метаданных конфигураций баз 1С 8.3.
Отображает свойства и реквизиты объектов конфигурации, их количество, основные права доступа и т.д.
Отображаемые характеристики объектов: свойства, реквизиты, стандартные рекизиты, реквизиты табличных частей, предопределенные данные, регистраторы для регистров, движения для документов, команды, чужие команды, подписки на события, подсистемы.
Отображает структуру хранения объектов базы данных, для регистров доступен сервис «Управление итогами».
Платформа 8.3, управляемые формы. Версия 1.1.0.83 от 24.06.2021

3 стартмани

Интеграция 1С и C#. Обращение к 1С через COM. Создание номенклатуры и выполнение запроса к 1С из C# на примере интеграции с Союз-PLM (система информационной поддержки жизненного цикла изделий). Обработка «Загрузка заказа на сборку». (ERP)

Союз-PLM представляет собой полнофункциональный программный комплекс для решения  широкого спектра задач управления инженерной технической информацией наукоемких изделий и сложных инженерных объектов в области машиностроения, приборостроения, архитектуры, строительства.

На практике, это управление конструкторской документацией, интегрированное с САПР, бизнес-процессы, файловый архив. Все это работает в SQL и шевелится с помощью скриптов на C#. Скрипты свободно  отлаживаются в MS Visual Studio. Подробнее смотрите на их сайте: http://www.programsoyuz.ru/products/system-soyuz-plm.html  Редактирование, конструирование и использование бизнес-процессов на порядок лучше систем на базе 1С из тех, что я изучил.

1 стартмани

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

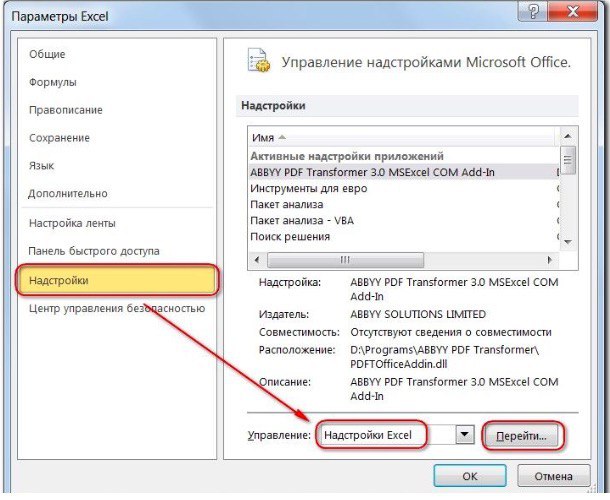
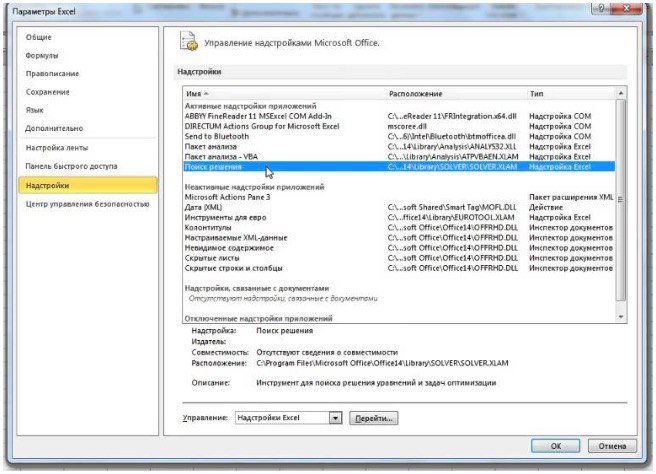
• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

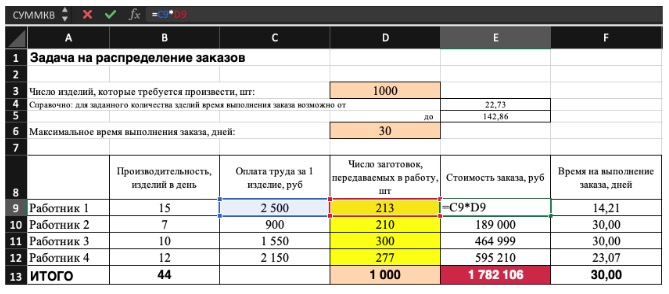
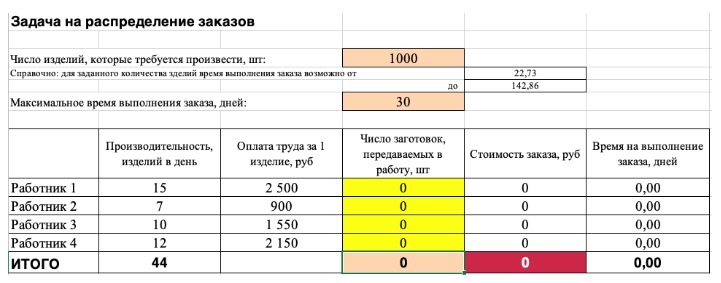
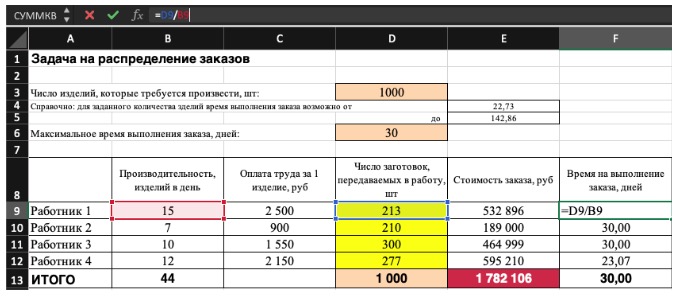
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.

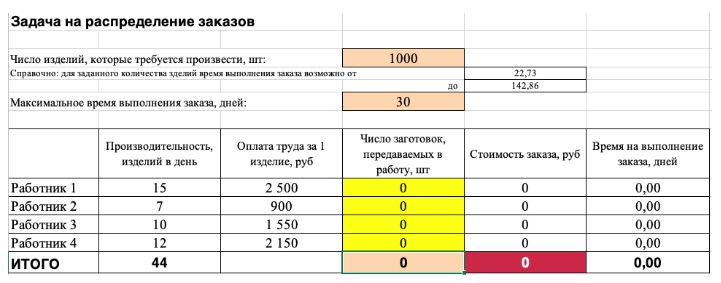
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

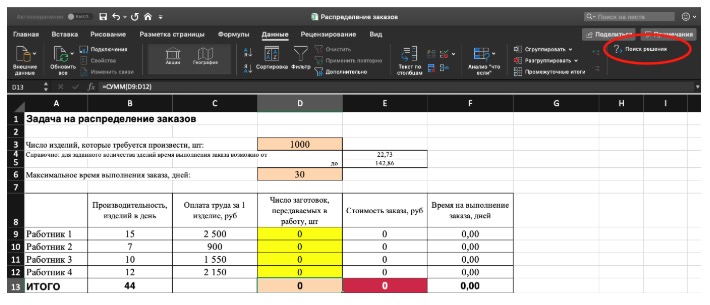
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Обработка текста, чисел и дат

Выделите ячейки с текстом, числами или датами и воспользуйтесь одной из 25 команд надстройки ЁXCEL. Объединяйте ячейки без потери данных, сжимайте пробелы, меняйте регистр, преобразуйте числа и даты в текст, преобразуйте текст в даты и числа. Быстро создавайте нумерованные списки, удаляйте непечатаемые символы, гиперссылки, примечания, условное форматирование и проверку данных из выделенных ячеек. Меняйте кириллицу на латиницу и наоборот. Извлекайте уникальные слова из текста, генерируйте сложные пароли, удаляйте или добавляйте слова, или символы к тексту выделенных ячеек. Вот только некоторые возможности надстройки ЁXCEL по обработки текста, чисел и дат.